数学_线性插值法

线性插值法（Linear Interpolation）是一种基于两点间线性关系的插值方法，用于在已知两个数据点之间估算未知点的数值。其核心思想是假设两个已知点之间的数据变化是线性的，从而通过直线方程进行估计。

数学公式

设已知两点为 $(x_0, y_0)$ 和 $(x_1, y_1)$，需要估算 $x$ 在区间 $[x_0, x_1]$ 内对应的 $y$ 值。

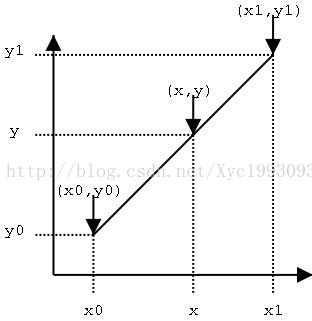
线性插值的公式为：

$$ y = y_0 + \frac{y_1 - y_0}{x_1 - x_0} \cdot (x - x_0) $$

或简化为：

$$ y = y_0 + (y_1 - y_0) \cdot \alpha \quad \text{其中} \quad \alpha = \frac{x - x_0}{x_1 - x_0} $$

计算步骤

1. 确定相邻点：找到 $x$ 所在的区间 $[x_0, x_1]$
2. 计算比例系数 $\alpha$（斜率）：表示 $x$ 在区间内的相对位置
3. 加权平均：基于 $\alpha$ 对 $y_0$ 和 $y_1$ 进行线性组合

应用示例

示例1：温度插值

已知时间与温度数据：

• 10:00 温度为 20°C ($x_0=10, y_0=20$)
• 12:00 温度为 26°C ($x_1=12, y_1=26$)

估算 11:00 的温度：

$$ \alpha = \frac{11-10}{12-10} = 0.5 \ y = 20 + (26-20) \cdot 0.5 = 23°C $$

示例2：分位点计算

数据集排序后为 $[1,3,5,7,9]$，计算 30% 分位点：

确定位置： $$ k = (5-1) \cdot 0.3 + 1 = 2.2 \quad \text{（非整数，需插值）} $$

取相邻值：第2个数为3，第3个数为5。

线性插值： $$ \alpha = 0.2 \ y = 3 + (5-3) \cdot 0.2 = 3.4 $$

应用场景

• 数据补全：填充缺失值（如时间序列数据）
• 图像处理：图像缩放时计算像素值（如双线性插值）
• 金融分析：估算资产价格或利率的中间值
• 工程计算：在离散数据点间生成连续曲线

优缺点

优点：

• 简单高效：计算速度快，适合实时应用
• 平滑性：结果连续，避免阶梯效应（相比最近邻插值）

缺点：

• 假设线性：若数据非线性变化，误差较大
• 不适用于外推：仅限已知数据区间内插值

Python实现

import numpy as np

# 已知点
x_known = [10, 12]
y_known = [20, 26]

# 插值点
x_new = 11
y_new = np.interp(x_new, x_known, y_known)
print(f"11:00 的温度为 {y_new}°C")  # 输出 23.0