AMM自动做市商

Uniswap GitHub：https://github.com/Uniswap

Uniswap V2 官网：https://app.uniswap.org/swap

Uniswap V3 白皮书：https://app.uniswap.org/whitepaper-v3.pdf

Uniswap V4 官网：https://v4.uniswap.org/

订单簿

传统的中心化交易说使用的订单簿的做市方式。

举一个栗子： 比如交易对金币/美元。此刻Alice希望10美元->1金币，Bob希望11美元->1金币。 Candy希望1金币->12美元。 这样就会形成一个订单簿，包含当前市场信息：

graph TD
    subgraph 订单簿 金币_美元
    
        subgraph 买方
            B1[买一: bob 11美元->1金币]
            B2[买二: alice 10美元->1金币]
        end
        subgraph 卖方
            S1[卖一: candy 1金币->12美元]
        end
    end

现在Devid急需用钱，他以市价卖出两个金币，那么bob和alice的挂单就会被成交。

交易信息也会被记录到订单簿中。

graph TD
    subgraph 订单簿 金币_美元
        subgraph 卖方
            S1[卖一: candy 1金币->12美元]
        end

        subgraph 成交记录
            T1[成交价: 10美元]
            T2[卖方: Devid 2金币 -> 21美元]
            T3[买方: bob 11美元->1金币]
            T4[买方: alice 10美元->1金币]
        end
    end

其中，alice和bob是被动成交的被成为maker。devid接受了他们的报价，被成为taker。 maker主要操作就是挂单和撤单，taker的主要操作是吃单，maker需要更低的手续费，taker需要更低的延迟等要求，目前区块链并不能很好要求。

AMM自动做市商

Uniswap项目提供了一种全新的做市解决方案。核心就一个公式（$k = x \times y$）（UniswapV2）。

示例

Alice认为当前1金币价值10美元，于是她创建了一个交易池，并且向池子中添加了10金币和100美元。

根据做市商算法： $$ k = x \times y $$ 计算得出： $$ k = 10 \times 100 = 1000 $$

流动性变化

Bob向池中添加了1金币，为了保持 $k$ 不变，池中美元数量需调整为： $$ \frac{k}{x} = \frac{1000}{11} \approx 90.91 \text{美元} $$ 因此，Bob获得了： $$ 100 - 90.91 = 9.09 \text{美元} $$ 相当于Bob以 1金币 兑换了 9.09美元。这样在没有订单簿的情况下也实现了一笔交易。 同时由于池子中金币变多了，美元变少了，相当于金币的价格变低了，实现了价格的变动。

在上面栗子中，Alice就是流动性提供者，Bob就是流动性使用者，交易池就是流动性池子。

Uniswap发展

上面的做市方式是在UniswapV2中实现的，但是很明显有一些问题。特别是在添加流动性池的时候，流动性被均匀添加到整个池子里面了（价格：0 ~ +∞）。但是实际情况，绝大部分流动性应该被添加到当前价位附近。

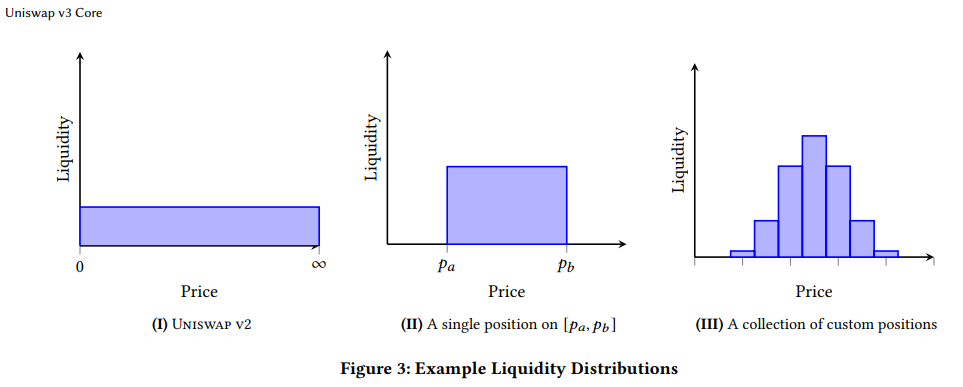
UniswapV3就解决了一个问题：

• UniswapV3允许添加流动性时指定价格范围。
• UniswapV3支持不同手续费的流动性池子。

UniswapV4？Uniswap V4 引入了一种名为“hooks”的新功能，这是一种智能合约，允许开发者在交易的不同阶段自定义池的行为。 这为动态费用、链上限价单以及将大额交易分散到时间上的系统等多种可能性打开了大门。底层架构也得到了改进，所有池现在都 housed 在一个单一的智能合约中（单例模式），使系统更高效且使用成本更低。

其他做市商

CPMM（Constant Product Market Maker，恒定乘积做市商）

核心公式：
[ x \cdot y = k ]
其中，( x ) 和 ( y ) 是流动性池中两种资产的数量，( k ) 为恒定常数。

特点：

• 价格由资产比例动态决定（如 ( P = y / x )）。
• 存在滑点（交易量越大，价格波动越明显）。
• 流动性永不枯竭（乘积恒定，但单边资产可能趋近于零）。

应用场景：主流代币交易（如 ETH/USDT）、长尾资产市场（如 MEME 币）。

---

CSMM（Constant Sum Market Maker，恒定总和做市商）

核心公式：

$$ x + y = k $$
其中，( x ) 和 ( y ) 是流动性池中两种资产的数量，( k ) 为常数。

特点：

• 价格固定为 1:1（如稳定币交易），滑点为零。
• 缺陷：当某一资产被大量购买时，可能导致另一种资产耗尽（流动性枯竭）。

应用场景：稳定币兑换（但因缺陷明显，实际应用较少）。

---

CLMM（Constant Liquidity Market Maker，恒定流动性做市商）

核心公式（简化版）：
$$ A \cdot (x + y) + x \cdot y = D $$
其中，$ A $ 是放大系数（调节滑点），$ D $ 是池中资产总值的函数。

特点：

• 在资产价格接近时（如稳定币），模拟恒定总和，滑点极低。
• 当价格偏离较大时，切换为恒定乘积（类似 Uniswap），避免流动性枯竭。

应用场景：稳定币或锚定资产交易（如 Curve 的 DAI/USDC/USDT 池）。

---

CMMM（Constant Mean Market Maker，恒定均值做市商）

核心公式：
$$ \prod_{i=1}^{n} x_i^{w_i} = k $$
其中，$ x_i $ 是第 $ i $ 种资产的数量，$ w_i $ 是其权重（满足 $ \sum w_i = 1 $），$ k $ 为常数。

特点：

• 支持多资产池（如 3 种以上）和自定义权重（如 Balancer 的 80/20 池）。
• 价格根据资产权重动态调整，灵活性高。

应用场景：多样化投资组合（如 Balancer 的多资产流动性池）。

---

对比总结

类型	公式	特点	典型应用
CSMM	$ x + y = k $	价格固定，易耗尽流动性	稳定币（理论场景）
CLMM	$ A(x + y) + xy = D $	低滑点混合模型	Curve 稳定币交易
CMMM	$ \prod x_i^{w_i} = k $	多资产、可定制权重	Balancer 多资产池

注：CLMM 的命名可能存在差异（如 Curve 的模型常被称为"混合型 AMM"），此处按问题要求归类。