算法(1)
《算法图解》
【《算法图解》chapter 01 - 算法简介】 https://www.bilibili.com/video/BV1Aw411U7mf/?share_source=copy_web&vd_source=5601c007f8bab5a1c68160f136bda449
引入
首先思考一个简单的问题,有100个有序的数字,现在需要猜一猜数字99是第几个数字?
最容易想到的方法就是从第1个开始,依次往后猜。如果运气好,第1个数字刚好是99,如果运气差,最后一个数字才是99。
这里就需要一个标准来衡量算法的性能,通常通过上界大O来衡量算法的性能,即最多需要多少步骤。专业术语就是时间复杂度。上述问题中,如果数字个数是N,最多需要猜N次,所以时间复杂度:O(N)。
当然,还有更好的方法,因为数字是有序的,我先猜中间位置的值,比如第50个数字,然后判断需要猜的数字val和这个数字的大小,如果大于val,我就猜第0个和第50个中间的数字,第25个,然后进一步缩小空间……依次类推,很快就能找到val的值。这就是二分查找法。
代码实现:
func binarySearch(arr []int, target int) int {
start, end := 0, len(arr)-1
for start <= end {
mid := (start + end) / 2
if target == arr[mid] {
return mid
} else if target > arr[mid] {
start = mid
} else {
end = mid
}
}
return -1 // -1 未找到
}
二分查找的时间复杂度为O(log₂N),其推导过程如下:
-
每次查找都将搜索范围减半:
- 初始范围:N
- 第一次查找后:N/2
- 第二次查找后:N/4
- …
- 第m次查找后:N/(2^m)
-
当搜索范围缩小到1时查找结束: N/(2^m) = 1 ⇒ 2^m = N ⇒ m = log₂N
因此,最坏情况下需要log₂N次查找操作,时间复杂度即为O(log₂N)。
基础数据结构
数组和链表是算法学习中最基础的数据,后面一些更加复杂数据结构,比如树和图,都是基于数组和链表构造的。
计算机内存原理
计算机内存可以想象成一个巨大的储物柜,每个储物格都有唯一的地址编号。这些储物格用于存储程序运行时的数据。
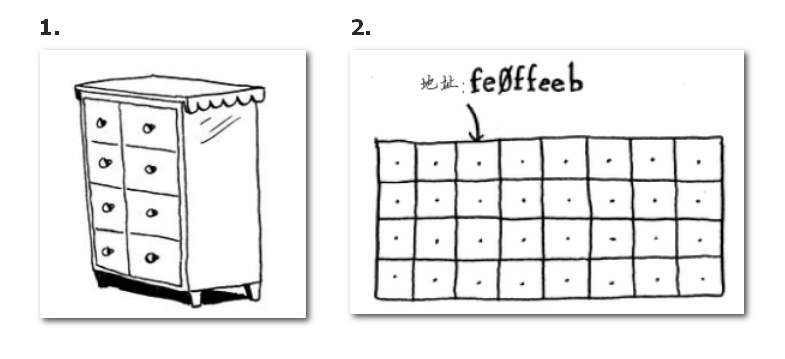
内存的几个关键特性:
- 随机访问:可以直接通过地址访问任意位置的数据,访问时间相同
- 线性结构:内存地址从0开始连续编号,形成线性地址空间
- 易失性:断电后存储内容会丢失(与硬盘等持久存储不同)
内存工作原理:
- 当程序需要存储数据时,操作系统会分配空闲的内存地址
- CPU通过内存控制器访问内存中的数据
- 数据以二进制形式(0和1)存储在内存单元中
- 每个内存单元通常为1字节(8bit)
数组和链表
现在有一串连续的数字,需要存储在计算机内存中,有以下两种方式:
- 连续存储,一个接一个的存储在连续的地址中。
- 链式存储,每个数字存储在不同的地址中,通过指针连接。
如果采用连续存储,需要先开辟一块连续的内存空间,然后依次存储数字。如果这串数字是动态增加的,存储达到连续内存空间的存储上限以后,则需要重新开辟内存空间,并进行数据迁移。
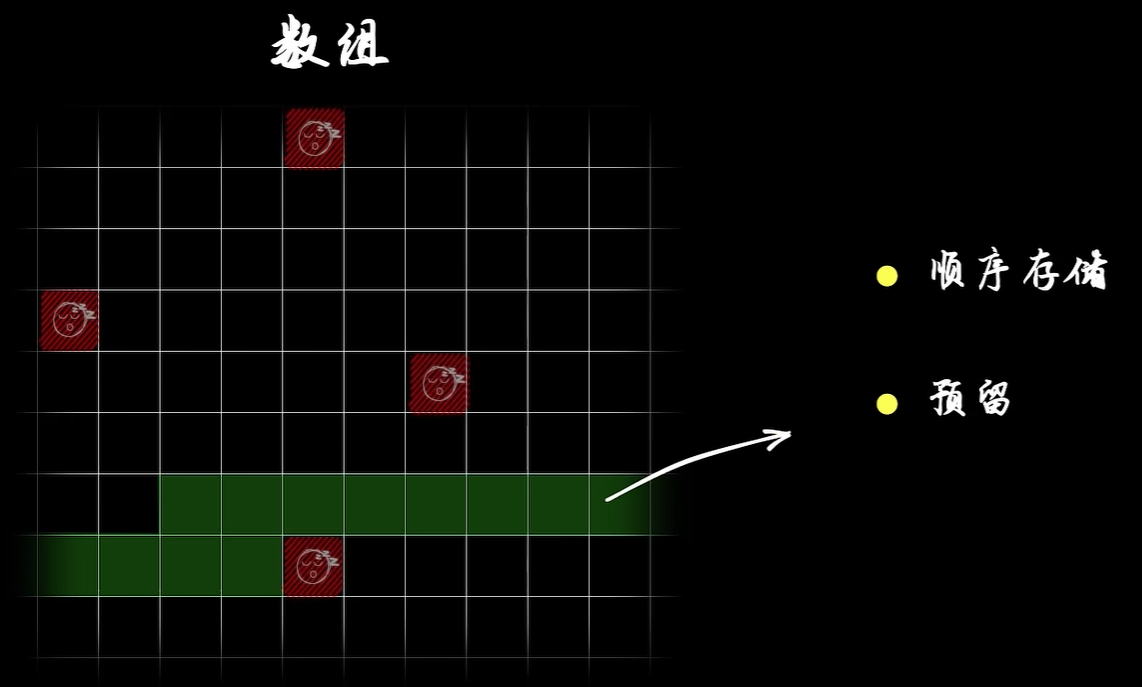
如果是链式存储则不存在这个问题,只需要在每个数字后面添加一个指针,指向下一个数字的地址。可以利用碎片的存储空间。
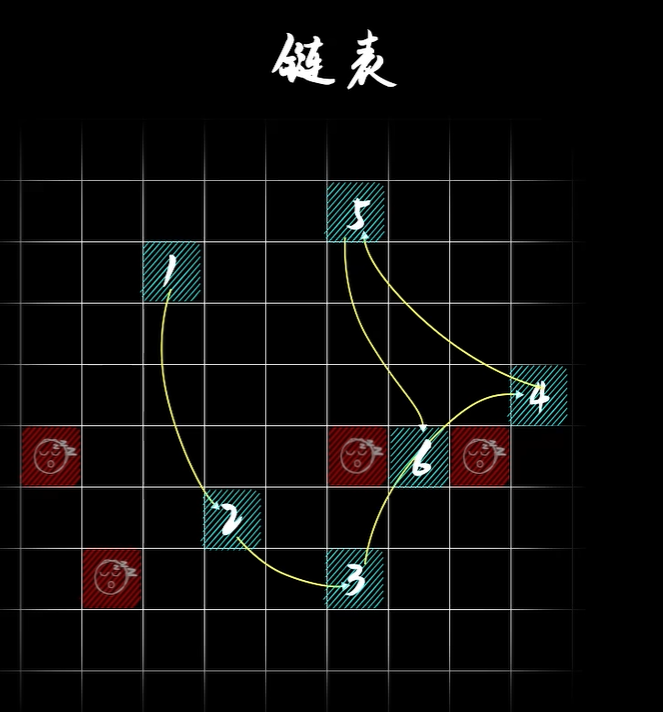
所以可以分析出,数组和链表的优缺点:
- 数组:
- 优点:随机访问,访问时间固定
- 缺点:需要连续内存空间,插入和删除操作需要移动大量数据
- 链表:
- 优点:不需要连续内存空间,插入和删除操作方便
- 缺点:不能随机访问,访问时间不固定
选择排序
有一串随机数字,list={5, 2, 9, 1, 7, 4, 6, 3, 8},现在需要进行排序,从大到小。
选择排序(Selection Sort)的基本逻辑是:
- 遍历整个列表,找到当前未排序部分中的最大(或最小)元素
- 将该元素与未排序部分的第一个元素交换位置
- 重复上述过程,每次处理未排序部分的子列表
代码实现:
func selectSort(arr []int) {
for i := range arr {
maxIndex := i
for j := i + 1; j < len(arr); j++ {
if arr[maxIndex] < arr[j] {
maxIndex = j
}
}
// swap maxIndex和i对应的数字
tmp := arr[i]
arr[i] = arr[maxIndex]
arr[maxIndex] = tmp
}
}
时间复杂度分析: 很容易可以分析出,第一次需要遍历N次,第二次需要遍历N-1次……最后一次需要遍历1次。
所以总次数:n + (n-1) + (n-2) + … + 1,这是一个典型的等差数列求和问题,每次遍历次数递减1,形成一个公差为-1的等差数列。
根据等差数列求和公式:总和 = (首项 + 末项) × 项数 ÷ 2,因此,我们可以得出总操作次数为 (n + 1) × n / 2 = n(n+1)/2。根据算法复杂度表示规范,我们保留最高阶项,最终时间复杂度表示为 O(n²)。
递归
Stack Overflow上有一句话:“如果使用循环,程序的性能可能会更高;如果使用递归,程序更容易理解。如何选择要看什么对你来说更重要。”
最佳实践通常是:优先使用递归,增加程序的可读性,如果程序不满足性能要求,则使用循环代替递归。
求阶乘实现
分析下面一个问题,如何求:5!?5! = 5 × 4 × 3 × 2 × 1
进一步分解:5! = 5 x 4! = 5 x 4 x 3!
如果是n!?n!=nx(n-1)x…x1=nx(n-1)!
所以,递归问题的核心就是将问题分解为更小的同类子问题。
整数n阶乘代码实现:
func fact(n int) int {
if n == 0 { // 基线条件
return 1
} else { // 递归条件
return n * fact(n-1)
}
}
编写递归函数时,必须告诉它何时停止递归,不然就会一直循环下去。每个递归函数都有两部分:基线条件和递归条件。
递归条件指函数调用自己,基线条件指函数不在调用自己的条件。
栈
栈是一种简单的数据结构,就子弹夹,先上的子弹会在弹夹底部,后上的子弹在弹夹顶部,开枪以后,弹夹顶部的子弹最先被打出。所以栈的特征就是:先进后出。区别于队列的先进先出。

调用栈
func hello1(name string) {
println("hello1 " + name)
hello2(name)
bye(name)
}
func hello2(name string) {
println("hello2 " + name)
}
func bye(name string) {
println("bye " + name)
}
当函数hello1()执行时,调用栈的工作流程如下:
- 首先将hello1()函数及其参数name压入调用栈
- 执行hello1()函数体,遇到hello2()调用时:
- 暂停hello1()当前执行状态(包括局部变量等)压入栈
- 将hello2()及其参数name压入栈顶
- hello2()执行完毕后从栈顶弹出
- 恢复hello1()的执行状态继续执行
- 遇到bye()调用时重复类似过程
递归调用栈
递归函数也使用调用栈,上面阶乘fact(3),调用栈图例:

我们会发现每一层递归调用都会入栈,直到遇到基线条件才会开始出栈。所以递归调用,更加消耗内存。
尾递归
尾递归是递归的一种特殊写法,核心是将中间结果作为参数传递,避免在递归返回时进行额外计算。 整数n阶乘代码实现:
func factTail(ret, n int) int {
if n == 0 { // 基线条件
return ret
} else { // 递归条件
return factTail(ret * n, n - 1) // 将乘法结果直接传递给下一次递归
}
}
// 包装函数,简化调用
func factorial(n int) int {
return factTail(1, n) // 初始 ret = 1
}
快速排序
分治
分而治之(divide and conquer, D&C)一种著名的递归式问题解决方法。分治法是递归的一种范式。
分治法一般分为两步:
- 把原有问题分解成若干子问题。
- 把子问题的答案合并成最后的结果。
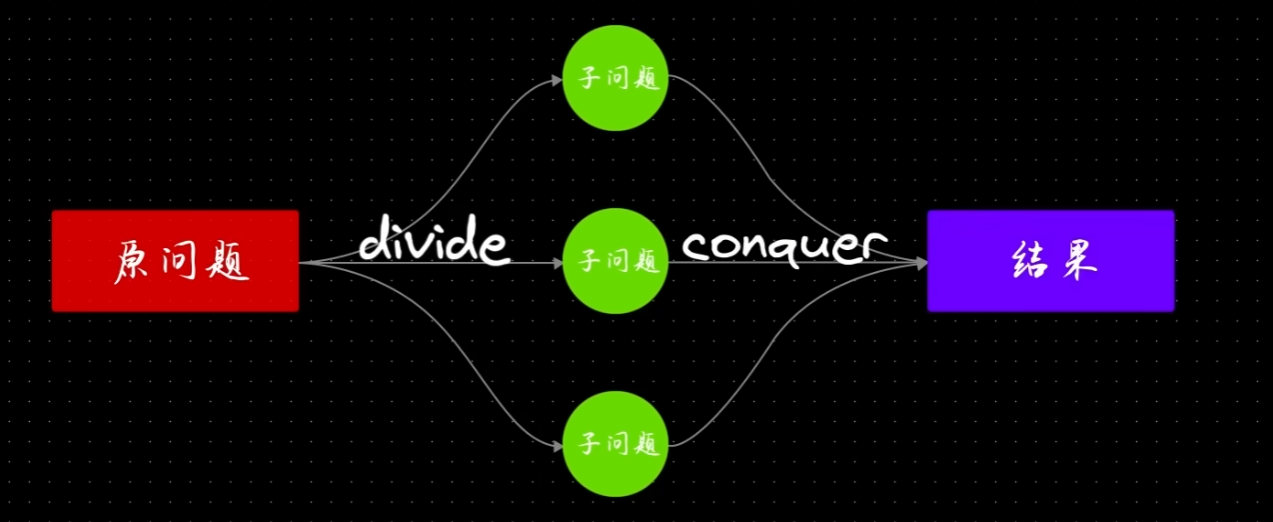
其实很多问题有固定的解,比如农田分割问题,这个问题和欧几里得算法中求两个数的最大公约数是同一个问题。对于没有多少数学天赋的我,直接叫我解决分割农田的问题,我是想不到答案的。我可能会尝试列一组方程式去求解,而想不到欧几里得算法。所以不必灰心,多积累吧,争取下次类似的问题能触类旁通。
农田分割问题
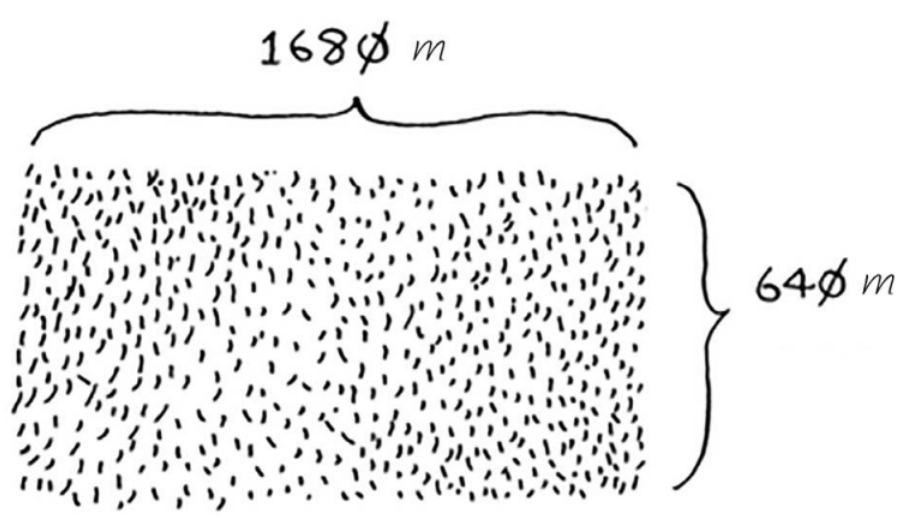
现在有一块农田,需要将它均匀地分成方块,且分出的方块尽可能大。现在,尝试用D&C策略来解决这个问题,D&C是递归的。所以,解决问题包括两个步骤:
- 找出基线条件。
- 不断将问题分解,直到符合基线条件。
解决方案:
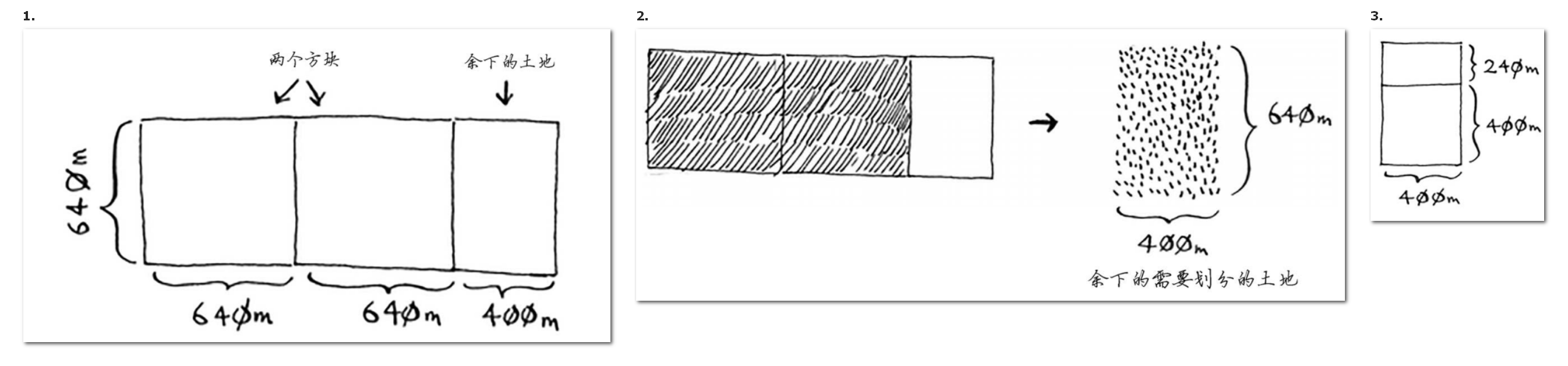

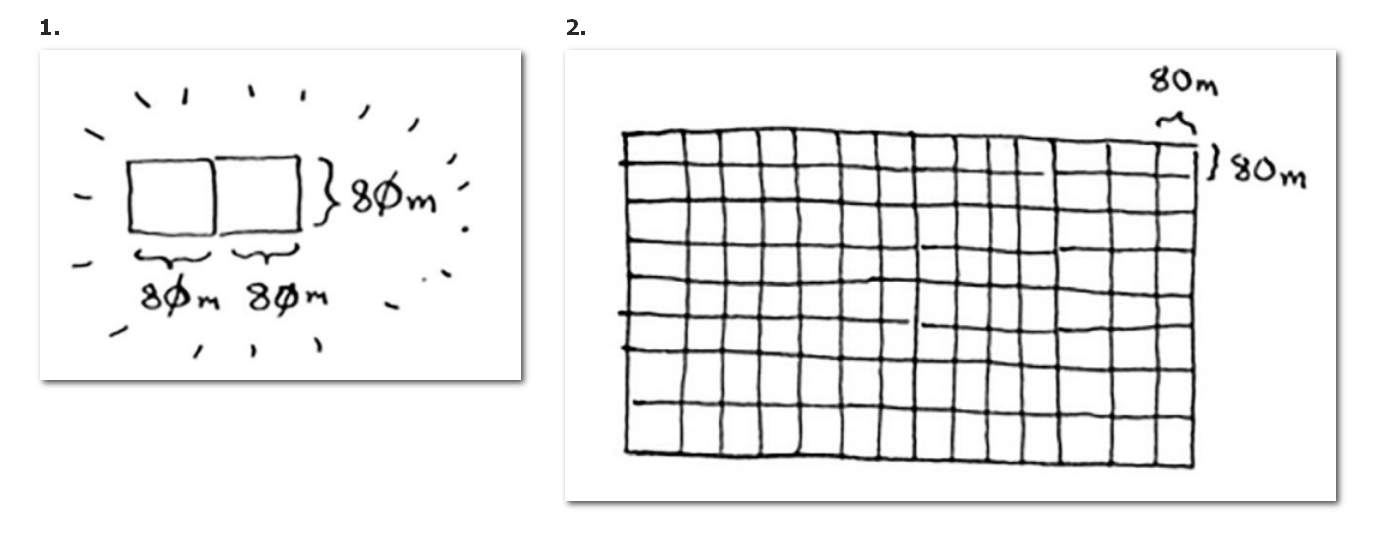
- 首先,把整块农田划分为宽*宽的方块,然后获得剩余的方块。即长 % 宽 = 168 % 64 = 40,剩余方块的大小就是宽 * 40,即64 * 40。
- 重复上述步骤,划分剩余方块,直到剩余方块就是一个正方形就停止。这个正方形就是最小方块。
回到递归问题:
- 基线条件,剩余方块:长 % 宽 = 0,即能被平分方块。
- 递归条件,剩余方块:长 % 宽 != 0。
- 递归操作:从大方块中,划分宽*宽的方块,获得剩余方块。
代码实现:
func farmlandSplit(length, width int) int {
if length%width == 0 { // 基线条件
return width
} else { // 递归条件
newWidth := length % width
return farmlandSplit(width, newWidth)
}
}
归并排序
归并排序使用的就是分治法。比如,需要对数字排序,首先把这段数据分为两半,给这两段数据排好序,再合并到一起就可以了。这样问题规模就缩小了。按照这个思想,继续分解数据,直到只剩下一个数字,不要排序为止。然后合并结果。
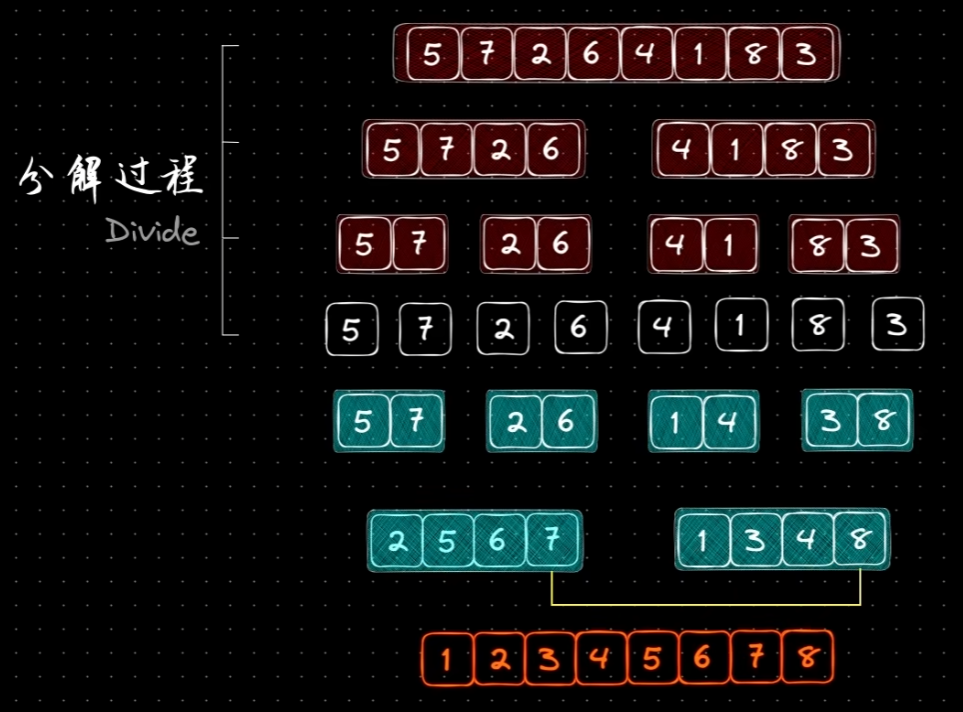
回到递归问题:
- 基线条件:数据只有一个,不需要排序,直接追加到结果中。
- 递归添加:数据数量大于一个。
- 递归操作:分半数据,归并操作。
代码实现:
- 如何合并两个有序数组? 使用双指针法,有序数组合并的是双指针法的经典案例。需要记忆。
/**
* 合并两个有序的数组
**/
func merge(left, right []int) []int {
ret := make([]int, 0, len(left)+len(right))
i, j := 0, 0
for i < len(left) && j < len(right) {
if left[i] <= right[j] {
ret = append(ret, left[i])
i++
} else {
ret = append(ret, right[j])
j++
}
}
ret = append(ret, left[i:]...)
ret = append(ret, right[j:]...)
return ret
}
- 归并排序实现
/**
*为什么ret要传递指针?因为go中切片是引用类型,传参是应用的拷贝。所以在函数内部修改切片,并不会直接影响到外层切片。
*
**/
func mergeSort(arr []int, ret *[]int) {
if len(arr) <= 1 { // 基线条件
*ret = append(*ret, arr...)
return
} else {
mid := len(arr) / 2
left := make([]int, 0, mid)
right := make([]int, 0, len(arr)-mid)
mergeSort(arr[0:mid], &left)
mergeSort(arr[mid:], &right)
*ret = merge(left, right)
}
}
时间复杂度分析:
- 分治过程:归并排序通过递归将数组分成两半,直到子数组长度为1(基线条件)。分治的层数为$\log_2{n}$(因为每次将问题规模减半)。(Tips:这种减半问题,比如归并排序,二分搜索等等时间复杂度为$\log_2{n}$,作为结论记住。)
- 合并过程:每一层需要合并 $n$ 个元素(所有子数组合并后的总长度为 $n$)。合并的时间复杂度为 $O(n)$。
- 总复杂度:$O(n) \times O(\log n) = O(n \log n)$
空间复杂度:
归并排序需要额外的空间存储临时数组,因此空间复杂度为 (O(n))(非原地排序)。
快速排序
快速排序同样使用的是分治法。

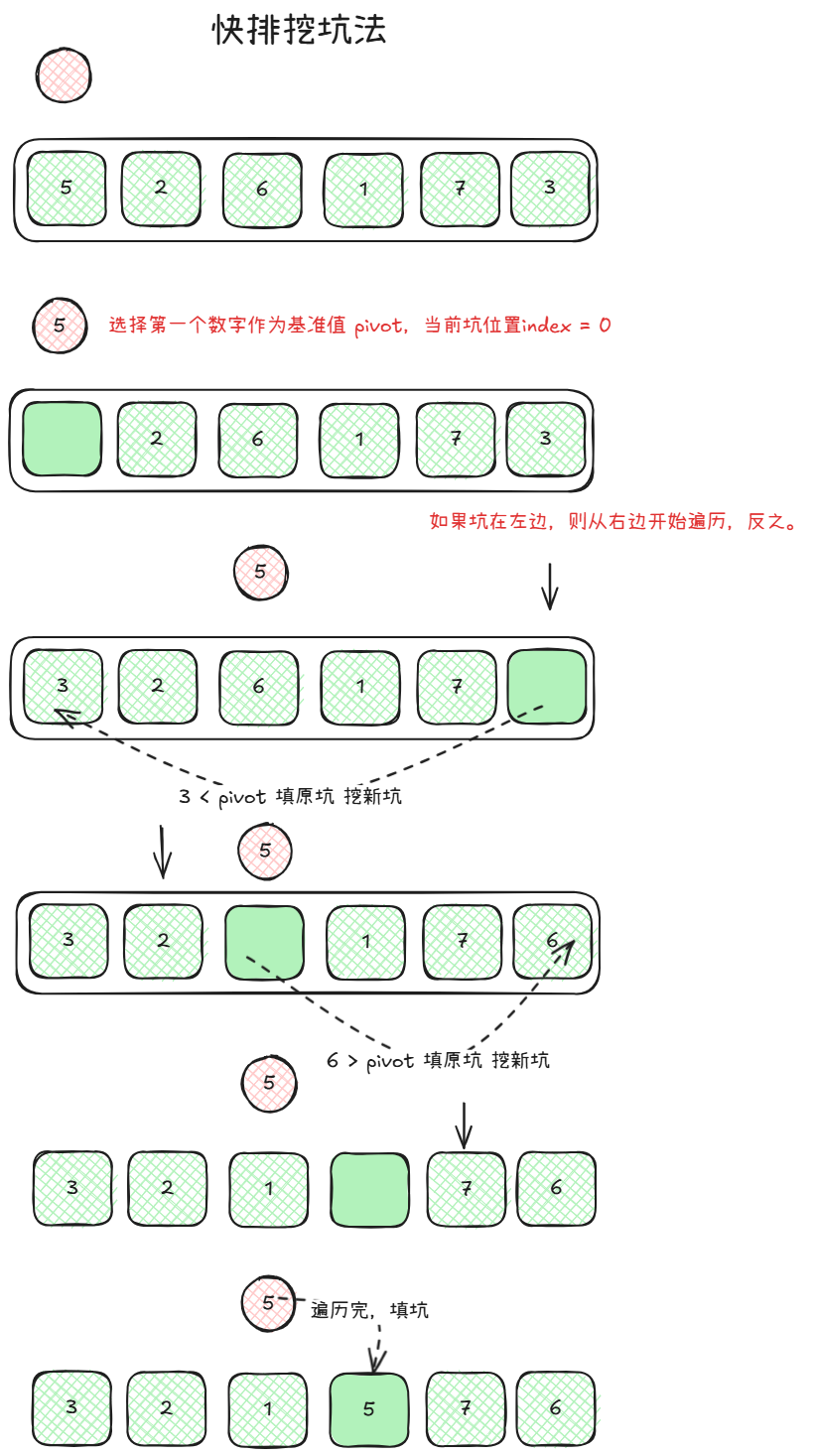
首先,随机选择一个数字,叫做基准数字,比如第一个数字5,然后保证左边的比5小,右边的比5大。 然后,左边和右边的数据执行相同的操作,最后得到的数组就是有序的数组。
回归递归问题:
- 基线条件:当子数组长度为 0 或 1 时,无需排序,直接返回。
- 递归条件:当子数组长度 ≥ 2 时,需进一步分解排序。
- 递归操作:分区->递归左子数组->递归右子数组
代码实现: 使用挖坑法实现:
func quickSort(arr []int) {
if len(arr) <= 1 {
return
}
pivot := arr[0] // 选取第一个值作为基准值
left, right := 0, len(arr)-1
for left < right {
for left < right && arr[right] >= pivot {
right--
}
if left < right {
arr[left] = arr[right]
left++
}
for left < right && arr[left] <= pivot {
left++
}
if left < right {
arr[right] = arr[left]
right--
}
}
arr[left] = pivot // 填坑
// 递归遍历左右子数组
quickSort(arr[:left])
quickSort(arr[left+1:])
}
时间复杂度分析:
- 正常情况下,类似于归并排序,把原数组分成两半简单数组,递归,存在减半操作,所以时间复杂度:O(logN)。
- 递归操作是一次循环,时间复杂度为:O(N)。
- 所以总的时间复杂度为:O(NlogN)。
- 极端情况:如果数据本来就是有序的,减半并没有真正减半,还是原数组,总时间复杂度:O(N*N)
快速排序 vs 归并排序:
大多数情况下快速排序的时间复杂度:O(NlogN + C1),归并排序的时间复杂度:O(NlogN + C2),但是由于快排是原地排序,并不需要多的额外内存空间,所以内存申请回收开销更小。即认为C1 < C2,特别是在数组特别大的情况下。但是快排在对相对有序的数据进行排序时,性能会退化。而且快排并不是稳定排序。

